jueves, 29 de enero de 2015

Fracciones Equivalentes




Publicadas por a la/s No hay comentarios.:

Denominador común

¡Esta es la manera más fácil que conozco de sumar o restar fracciones!

¿Qué es un Denominador?

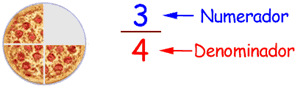fracción El denominador es el número de abajo en una fracción.

Muestra en cuántas partes iguales se divide la cosa

 

¿Qué es un denominador común?

Denominador "común" sólo quiere decir que los denominadores de dos (o más) fracciones son comunes, o sea el mismo.

 

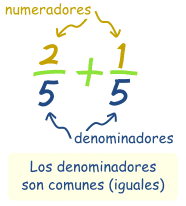 denominador común

¿Por qué es importante?

Sumar y restar fracciones

Antes de poder sumar o restar fracciones, las fracciones deben tener un denominador común (es decir, los denominadores deben ser iguales).

Hacer iguales los denominadores

Si los denominadores no son iguales, puedes usar el método del mínimo común denominador para hacerlos iguales, o puedes:
Multiplicar cada fracción por el denominador de la otra
Publicadas por a la/s No hay comentarios.:

Mínimo denominador común

... es el Mínimo común múltiplo de los denominadores...
Primero, vamos a recordar lo que es el denominador:

Fracciones

Una fracción (como 3/4) tiene dos números:
Numerador

Denominador
Al número de arriba lo llamamos Numerador, es el número de partes que tienes.
Al de abajo lo llamamos Denominador, es el número de partes en que se ha dividido el total.

Fracciones con denominadores diferentes

A veces tienes dos (o más) fracciones con denominadores diferentes - a lo mejor quieres sumarlas o restarlas - pero necesitas tener los mismos denominadores antes de poder hacerlo:

Ejemplo: ¿Cuánto es 3/8 + 5/12 ?

Vamos a probar a hacer que los denominadores sean el mismo... si multiplicas 8 × 3 sale 24, y su multiplicas 12 × 2 también sale 24. Así que probemos con eso (importante: lo que hagas abajo, debes hacerlo también arriba):
  × 3  
3  =  9


8 24
  × 3  
y,
  × 2  
5  =  10


12 24
  × 2  
Ahora podemos sumar: 9/24 + 10/24 = 19/24.

Cómo poner el mismo denominador

El truco es calcular el Mínimo común múltiplo de los denominadores. (Lee sobre el Mínimo común múltiplo ahora si no lo has hecho todavía.)

En el ejemplo de antes, el mínimo común múltiplo de 8 y 12 era 24. Y por eso el mínimo común denominador de 3/8 y 5/12 es 24
Así que, aquí están los pasos:
  • Calcula el mínimo común múltiplo de los denominadores (se le llama el mínimo común denominador).
  • Cambia cada fracción (usando fracciones equivalentes) para que los denominadores sean iguales al mínimo común denominador.
  • ¡Ya puedes hacer lo que quieras con las fracciones (sumar, restar)!
 

Ejemplo: ¿Cuánto es 1/6 + 7/15 ?

El mínimo común mútiplo de 6 y 15 es 30 (¡intenta calcularlo tú mismo!). Así que vamos a multiplicar para que cada denominador sea igual a 30:
  × 5  
1  =  5


6 30
  × 5  
y,
  × 2  
7  =  14


15 30
  × 2  
Ahora es fácil hacer la suma: 5/30 + 14/30 = 19/30.

 

Herramienta para el mínimo común múltiplo

Para calcular automáticamente el mínimo común denominador, puedes usar nuestra Herramienta para el mínimo común múltiplo - sólo pon los denominadores, pulsa el botón, y te saldrá el mínimo común denominador.
Publicadas por a la/s No hay comentarios.:

Fracciones

Una fracción es una parte de un total

Corta una pizza en trozos, y tendrás fracciones:

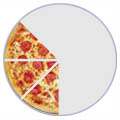1/2 1/4 3/8
(Una mitad)
(Un cuarto)
(Tres octavos)
     
El número de arriba te dice cuántas porciones tienes y el de abajo te dice en cuántos trozos se ha cortado la pizza.

Numerador / Denominador

Al número de arriba lo llamamos Numerador, es el número de partes que tienes.
Al de abajo lo llamamos Denominador, es el número de partes en que se ha dividido el total.

Numerador

Denominador
¡Sólo tienes que recordar esos nombres! (Si los confundes, recuerda que denominador es con "D" de dividir)

Fracciones equivalentes

Algnas fracciones parecen diferentes pero en realidad son la misma, por ejemplo:

  4/8 = 2/4 = 1/2  

(Cuatro octavos)   (Dos cuartos)   (Una mitad)  
       
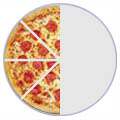Normalmente lo mejor es dar la respuesta usando la fracción más simple (1/2 en este caso). Eso se llama Simplificar o Reducir la fracción.

Sumar fracciones

Puedes sumar fracciones fácilmente si el número de abajo (el denominador) es el mismo:
  1/4 + 1/4 = 2/4 = 1/2  
  (Un cuarto)   (Un cuarto)   (Dos cuartos)   (Una mitad)  
         
Otro ejemplo:
  5/8 + 1/8 = 6/8 = 3/4  
         

Sumar fracciones con denominadores diferentes

¿Y si los denominadores no son iguales? Como en este ejemplo:

  3/8 + 1/4 = ?      
         

Deberías hacer que los denominadores fueran iguales de alguna manera. En este caso es fácil, porque sabemos que 1/4 es lo mismo que 2/8 :

  3/8 + 2/8 = 5/8      
         
Publicadas por a la/s No hay comentarios.:

miércoles, 28 de enero de 2015

Fracción unitaria

Una fracción unitaria es una fracción común en la cual el numerador es igual a 1 y el denominador es un entero positivo:  1/2 \; , \ 1/3 \; , \ 1/4\; , \dots\  Las fracciones unitarias son losrecíprocos multiplicativos de los números naturales (es decir de los enteros positivos).
  • Ejemplos:
La serie armónica: \frac11+\frac12+\frac13+\cdots
La serie geométrica: \frac{1}{2} \,+\, \frac{1}{4} \,+\, \frac{1}{8} \,+\, \frac{1}{16} \,+\, \cdots
Las fracciones egipcias son otro ejemplo de aplicación de las fracciones unitarias.

Fracción egipcia


Se le llama fracción egipcia al tipo de representación de fracciones utilizado en el Antiguo Egipto. Una fracción común -positiva- se escribe por medio de una suma de fracciones unitarias distintas, es decir que ninguno de los sumandos tiene el mismo denominador.
Ejemplos:
  • \frac{5}{121}=\frac{1}{33}+\frac{1}{121}+\frac{1}{363}
  • \frac{19}{20} = \frac{1}{2}+\frac{1}{3}+\frac{1}{9}+\frac{1}{180}
  • \frac{19}{20} = \frac{1}{2}+\frac{1}{4}+\frac{1}{5}
Todo número racional positivo se puede expresar como suma de fracciones unitarias (es decir, como fracción egipcia), si bien la representación no es única, como se aprecia en el ejemplo. Las fracciones egipcias fueron utilizadas también por los matemáticos griegos y durante la Edad Media. El matemático medieval Fibonacci (en su Liber abaci) describe su uso y las desarrolla dentro del marco moderno de las series matemáticas.

El ojo de Horus (Udyat) contiene los símbolos jeroglíficos de los primeros números racionales.

Publicadas por a la/s 1 comentario:

Fracción decimal

Una fracción decimal es una fracción del tipo \frac{a}{10^n}, es decir, una fracción cuyo denominador es una potencia de 10. Por convención, se toma a positiva. Las fracciones decimales suelen expresarse sin denominador, con uso del separador decimal, es decir, como número decimal exacto (Por ejemplo: 8/10, 83/100, 83/1000 y 8/10000 se escriben 0.8, 0.83, 0.083 y 0.0008). Inversamente, un número decimal finito (o un entero) puede escribirse como fracción decimal simplemente multiplicando por un potencia apropiada de \frac{10^n}{10^n} (Por ejemplo: 1=10/10 1.23=123/100). Una fracción decimal no es necesariamente irreducible.
Se cree que las fracciones decimales eran conocidas por los matemáticos chinos en el siglo I, y que de ahí se extendió su uso a medio Oriente y Europa. J. Lennart Berggren nota que un sistema posicional con fracciones decimales fue utilizado por el matemático árabe Abu'l-Hasan al-Uqlidisi en el siglo X.
Khwarizmi introduce las fracciones al mundo islámico a comienzos del siglo IX. Su representación de las fracciones está tomada de la matemática tradicional china. Esta forma de escritura de las fracciones con el numerador arriba y el denominador abajo, sin barra horizontal, fue utilizada también en el siglo X por Abu'l-Hasan al-Uqlidisi y en el siglo XV por Jamshīd al-Kāshī en su trabajo La llave aritmética.
El uso moderno fue definitivamente introducido por Simon Stevin en el siglo xvi.

Fracción continua


Se llama fracción continua de orden n a una expresión de la forma:
x = a_0 + \cfrac {1} {a_1 + \cfrac {1} {a_2 + \cfrac {1} { \begin{array}{l} \ddots \\ {a_{n-2} + \cfrac {1} {a_{n-1} + \cfrac {1} {a_n} } } \end{array} } } }
En donde (a_0, a_1, a_2, a_3, ..., a_k, ...)\  es una sucesión de enteros positivos.
Publicadas por a la/s No hay comentarios.:

Historia

En el Antiguo Egipto se calculaba utilizando fracciones cuyos denominadores son enteros positivos; son las primeras fracciones utilizadas para representar las «partes de un entero», por medio del concepto de recíproco de un número entero. Esto equivale a considerar fracciones como: un medio, un tercio, un cuarto, etc., de ahí que las sumas de fracciones unitarias se conozcan como fracción egipcia. Se puede demostrar además, que cualquier número racional positivo se puede escribir como fracción egipcia. El jeroglífico de una boca abierta 
D21
 denotaba la barra de fracción (/), y un arte numérico escrito debajo de la "boca abierta", denotaba el denominador de la fracción.
Los babilonios utilizaban fracciones cuyo denominador era una potencia de 60. El sistema chino de numeración con varillas permitía la representación de fracciones. Los griegos yromanos usaron también las fracciones unitarias, cuya utilización persistió hasta la época medieval. Diofanto de Alejandría (siglo IV) escribía y utilizaba fracciones. Posteriormente, se introdujo la «raya horizontal» de separación entre numerador y denominador, y el numerador dejó de restringirse al número uno solamente, dando origen a las llamadas fracciones vulgares o comunes. Finalmente, se introducen las «fracciones decimales», en donde el denominador se escribe como una potencia de diez.
Khwarizmi introduce las fracciones en los países islámicos en el siglo IX. La forma de representar las fracciones provenía de la representación tradicional china, con el numerador situado sobre el denominador, pero sin barra separadora. Leonardo de Pisa (Fibonaccci) en su Liber Abaci (Libro del Ábaco ), escrito en 1202, expone una teoría de los números fraccionarios. Las fracciones se presentan como fracciones egipcias, es decir, como suma de fracciones con numeradores unitarios y denominadores no repetidos.

Cronología
AñoAcontecimiento
1800 a. C.Registro de uso de fracciones por el Imperio Babilónico.
1650 a.C.Sistema de fracciones egipcias.
500-600 d.C.Aryabhata y Brahmagupta desarrollan las fracciones unitarias.
100Sistema chino de cálculo de fracciones con varillas (Suanpan).
1202Fibonacci difunde la notación con barra para separar numerador y denominador.
1585Teoría sobre las fracciones decimales de Simon Stevin.
1700Uso generalizado de la línea fraccionaria (barra horizontal u oblícua).
Publicadas por a la/s No hay comentarios.:
Suscribirse a: Entradas (Atom)